Mathematics
Excelente: timeline of mathematic: https://mathigon.org/timeline
Mathematics includes the study of such topics as quantity (number theory), structure (algebra), space (geometry), and change (mathematical analysis). It has no generally accepted definition.
- https://es.wikipedia.org/wiki/Matem%C3%A1ticas
- https://en.wikipedia.org/wiki/Mathematics#cite_note-Mura-7
- Number theory (or arithmetic)
- Linear algebra https://en.wikipedia.org/wiki/Linear_algebra
- Linear algebra is the branch of mathematics concerning linear equations, linear maps, and their representations in vector spaces and through matrices.
- Mathematical analysis (Math of change) https://en.wikipedia.org/wiki/Mathematical_analysis
- Analytic geometry https://en.wikipedia.org/wiki/Analytic_geometry
- Infinitesimal calculus (Math of change) (The study of things that change) https://en.wikipedia.org/wiki/Calculus
- Differential calculus (Derivative) https://en.wikipedia.org/wiki/Differential_calculus
- Integral calculus https://en.wikipedia.org/wiki/Integral
- Fundamental theorem of calculus https://en.wikipedia.org/wiki/Fundamental_theorem_of_calculus
- One of the applications of Mathematical analysis (Calculus in particular) is for Signal processing
- Applied mathematics: Some disciplines are considered to be applied mathematics. Sin embargo, no me queda claro si las área que estoy enumerando aquí realmente forman parte de lo que se conoce como Applied mathematics. En particular, Statistics can be considered to be a distinct mathematical science rather than a branch of mathematics. https://en.wikipedia.org/wiki/Statistics
- Discrete mathematics https://en.wikipedia.org/wiki/Discrete_mathematics
- Numerical analysis https://en.wikipedia.org/wiki/Numerical_analysis
- Computer algebra https://en.wikipedia.org/wiki/Computer_algebra
- Statistics https://en.wikipedia.org/wiki/Statistics
- Applications of mathematics:
-
- One of the applications of Mathematical analysis (Calculus in particular) is for Signal processing.
Contents
Numbers
https://en.wikipedia.org/wiki/Real_number
- Real numbers () include the rational numbers (), which include the integers (), which in turn include the natural numbers ()
- : A real number is a value of a continuous quantity that can represent a distance along a line (or alternatively, a quantity that can be represented as an infinite decimal expansion). https://en.wikipedia.org/wiki/Real_number
- : A rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator , and a non-zero denominator . https://en.wikipedia.org/wiki/Rational_number
- Numbers like or cannot be expressed as the ratio of two integers, but can be represented on real number line. https://socratic.org/questions/what-is-the-difference-between-real-numbers-and-rational-numbers
What is a function
https://en.wikipedia.org/wiki/Function_(mathematics)
Diagram of a function, with domain and codomain , which is defined by the set of ordered pairs . The image/range is the set . Taken from https://en.wikipedia.org/wiki/Function_(mathematics)
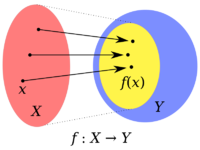
A function from to . The blue oval is the codomain of . The yellow oval inside is the image of . The term range is sometimes ambiguously used to refer to either the codomain or image of a function. Taken from https://en.wikipedia.org/wiki/Codomain
- In mathematics, a function is a binary relation over two sets that associates every element of the first set, to exactly one element of the second set.
- Intuitively, a function is a process that associates each element of a set , to a single element of a set .
- Formally, a function from a set to a set is defined by a set of ordered pairs such that and .
- and are resctively called the domain and the codomain of the function . The term range is sometimes ambiguously used to refer to either the codomain or image of a function [See https://en.wikipedia.org/wiki/Codomain]
- is called the graph of the function. In mathematics, the graph of a function is the set of ordered pairs , where .
- In mathematically we usually write
- We say is a function of
- Which means that mathematically depends on .
- So, as in this case, the independent variable is often designated by . The dependent variable is often designated by .
- A basic example of a function: Linear Functions: https://en.wikipedia.org/wiki/Linear_function
- Where and are constants. is frequently referred to as the slope of the line, and as the intercept.
- and ℝ
|
Continuity
- A rigorous definition of continuity of real functions is usually given in a first course in calculus in terms of the idea of a limit. First, a function f with variable x is said to be continuous at the point c on the real line, if the limit of f(x), as x approaches that point c, is equal to the value f(c); and second, the function (as a whole) is said to be continuous, if it is continuous at every point. A function is said to be discontinuous (or to have a discontinuity) at some point when it is not continuous there. These points themselves are also addressed as discontinuities. https://en.wikipedia.org/wiki/Continuous_function

- A sequence of continuous functions fn(x) whose (pointwise) limit function f(x) is discontinuous. The convergence is not uniform. https://en.wikipedia.org/wiki/Continuous_function
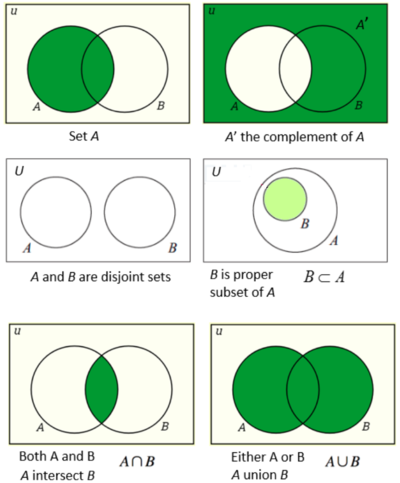
Union - Intersection - Complement
https://courses.lumenlearning.com/math4libarts/chapter/union-intersection-and-complement
Fourier series
This video is just amazing: But what is a Fourier series? From heat flow to drawing with circles | DE4 https://www.youtube.com/watch?v=r6sGWTCMz2k&vl=en
https://en.wikipedia.org/wiki/Fourier_series