Geophysics
Geophysics is a discipline that uses different areas of knowledge, such as physics, mathematics, and geology to study the internal constitution and history of the Earth. One of the applications of Geophysics is in oil exploration.
Seismic exploration:
The purpose of seismic exploration is to create an image of the subsurface and to estimate the distribution of a range of properties - in particular, the fluid or gas content. https://www.geos.ed.ac.uk/seismic/acq-proc/
Seismic exploration is based on the same physical principles of an ultrasound Echo Sonogram. So the same way as we use sound waves to generate an image of the internal structures of the body. For example, in the case of a pregnant woman to see the baby inside her belly, we can use seismic waves to obtain an image of the subsurface (the internal structure of the earth).
So in the case of Seismic exploration, we generate seismic waves from an explosion that we detonated on the surface of the earth (using Dynamite - TNT, for example). So this explosion generates waves that propagate into the subsurface, reflex in the layers of the subsurface, and come back to the surface. On the surface, we place wave detectors (called geophones) that are able to measure ground movement caused by the seismic waves generated in the shot (dynamite explosion). The ground motions are recorded as a function of time and thus we build what is knows as a seismogram, but commonly called a seismic trace in Seismic exploration. We can say that a seismogram is basically a representation of a seismic wave. In other words, a seismogram (seismic trace) is a time series of ground motion values (the ground motion values recorded are typically called the amplitude and it is a value between -1 and 1).
Then, using many seismic traces recorded in a study area we are able to build an image of the subsurface.
So, suppose that we are performing a Seismic acquisition survey where we want to cover an area of , we place geophones every , and we performed 80 shots. In every shot, each geophone is going to measure ground motion for 5 seconds and we will record this ground motion every .
With these acquisition parameters, we have around 400 geophones. For each geophone, we will have one seismogram for each shot. So we will have seismograms. In this particular case, we are recording ground motion values every during , so we well have amplitude values for each of the traces in our data. So, as you can see we have quiet lot of data here.
Signals are functions of time, space, or both time and space, carrying information. https://www.sciencedirect.com/topics/engineering/function-of-time
A seismogram, which is a representation of a seismic wave, is basically a kind of signal. Like for any other signal such as audio, radio waves, light waves, and even images, there is a large family of signal processing techniques that allows interpreting and extracting information from the signal.
The mathematical representation of signals and hence Signal processing is based on Mathematical Analysis (Calculus in particular). Some of the most important mathematical concepts that are applied to Signal processing are:
- File:Aplicaciones Geofisicas de los filtros digitales-Mario Caicedo-Milagrosa Aldana.pdf -- It's been downloaded from this link [Mario Caicedo & Milagrosa Aldana]
- https://courses.helsinki.fi/fi/geom_s2074
- Fourier analysis: Several signal processing techniques consists of Fourier-transforming a signal, manipulating the Fourier-transformed data in a simple way, and reversing the transformation. Fourier analysis can isolate individual components of a compound waveform, concentrating them for easier detection or removal https://en.wikipedia.org/wiki/Mathematical_analysis#Signal_processing
- Fourier transform https://en.wikipedia.org/wiki/Fourier_transform
- Time-frequency analysis https://en.wikipedia.org/wiki/Time%E2%80%93frequency_analysis
- Time-frequency analysis in Seismic processing:
- A set of mathematical formulas used to convert a time function, such as a seismic trace, to a function in the frequency domain (Fourier analysis) and back (Fourier synthesis). The Fourier transform is used extensively in signal processing to design filters and remove coherent noise. Many filtering operations are performed in the frequency domain. The Fourier transform has applications in image analysis and in pattern recognition in geological systems. https://www.glossary.oilfield.slb.com/en/Terms/f/fourier_transform.aspx#:~:text=A%20set%20of%20mathematical%20formulas,and%20back%20(Fourier%20synthesis).&text=The%20Fourier%20transform%20is%20used,filters%20and%20remove%20coherent%20noise.
- Fourier series: a Fourier series is a periodic function composed of harmonically related sinusoids, combined by a weighted summation. With appropriate weights, one cycle (or period) of the summation can be made to approximate an arbitrary function in that interval (or the entire function if it too is periodic). As such, the summation is a synthesis of another function. The discrete-time Fourier transform is an example of a Fourier series. https://en.wikipedia.org/wiki/Fourier_series
- Convolution and Correlation:
- Deconvolution:
- Discrete signals:
- Transformada de Fourier Discreta
- Convolución y Correlación de señales discretas
- Seismic Acquisition
- Procesamiento sísmico
- Interpretación Sísmica
- Seismic imaging
- Seismic Unix
Well logging
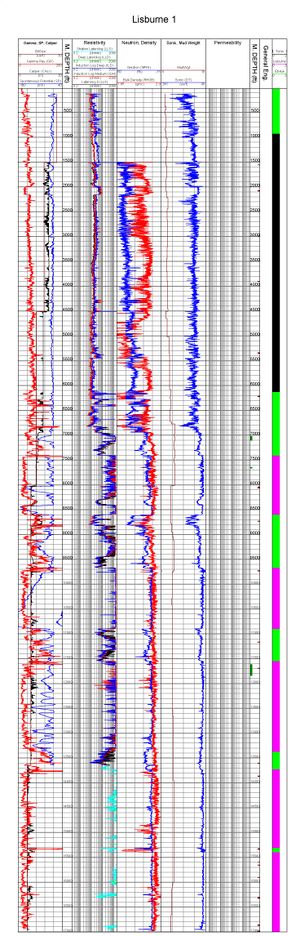
An well-log is a record of measurements of physical properties of the geologic formations (the rocks in the subsurface) penetrated by a borehole. In other words, a well-log is a record of measurements of physical properties of the rocks as a function of depth. Some of the physical properties that are measured are: Resistivity, Natural radioactivity of the rocks-formations (Gamma Ray Log). Because radioactive elements tend to be concentrated in shales, the Gamma-ray log normally reflects the shale content of the formation. Sound wave velocity: measurement of the time required for a sound wave to travel a constant distance. The principle is that velocity of the rock decrease when the porosity increase.
- Sonic Log: https://www.youtube.com/watch?v=e1ISSNcyWMw
- Gamma Ray Log: https://www.youtube.com/watch?v=pAgeGGbgXpM






