Página de pruebas 3
Contents
Naive Bayes
Multinomial Naive Bayes: https://www.youtube.com/watch?v=O2L2Uv9pdDA
Gaussian Naive Bayes: https://www.youtube.com/watch?v=uHK1-Q8cKAw https://www.youtube.com/watch?v=H3EjCKtlVog
https://www.youtube.com/watch?v=Q8l0Vip5YUw
https://www.youtube.com/watch?v=l3dZ6ZNFjo0
https://en.wikipedia.org/wiki/Naive_Bayes_classifier
https://scikit-learn.org/stable/modules/naive_bayes.html
Noel's Lecture and Tutorial: https://moodle.cct.ie/mod/scorm/player.php?a=4¤torg=tuto&scoid=8&sesskey=wc2PiHQ6F5&display=popup&mode=normal
Note, on all the Naive Bayes examples given, the Performance operator is Performance (Binomial Classification)
Naive Bayes classifiers are a family of "probabilistic classifiers" based on applying the Bayes' theorem to calculate the conditional probability of an event A given that another event B (or many other events) has occurred.
The Naïve Bayes algorithm is named as such because it makes a couple of naïve assumptions about the data. In particular, it assumes that all of the features in a dataset are equally important and independent [strong independence assumptions between the features «naïve» (features are the conditional events)]
These assumptions are rarely true in most of the real-world applications. However, in most cases when these assumptions are violated, Naïve Bayes still performs fairly well. This is true even in extreme circumstances where strong dependencies are found among the features.
Bayesian classifiers utilize training data to calculate an observed probability for each class based on feature values (the values of the conditional events). When such classifiers are later used on unlabeled data, they use those observed probabilities to predict the most likely class, given the features in the new data.
Due to the algorithm's versatility and accuracy across many types of conditions, Naïve Bayes is often a strong first candidate for classification learning tasks.
Bayesian classifiers have been used for:
- Text classification:
- Spam filtering: It uses the frequency of the occurrence of words in past emails to identify junk email.
- Author identification, and Topic modeling
- Weather forecast: The chance of rain describes the proportion of prior days with similar measurable atmospheric conditions in which precipitation occurred. A 60 percent chance of rain, therefore, suggests that in 6 out of 10 days on record where there were similar atmospheric conditions, it rained.
- Diagnosis of medical conditions, given a set of observed symptoms.
- Intrusion detection and anomaly detection on computer networks
Probability
The probability of an event can be estimated from observed data by dividing the number of trials in which an event occurred by the total number of trials.
- Events are possible outcomes, such as a heads or tails result in a coin flip, sunny or rainy weather, or spam and not spam email messages.
- A trial is a single opportunity for the event to occur, such as a coin flip, a day's weather, or an email message.
- Examples:
- If it rained 3 out of 10 days, the probability of rain can be estimated as 30 percent.
- If 10 out of 50 email messages are spam, then the probability of spam can be estimated as 20 percent.
- The notation is used to denote the probability of event , as in
Independent and dependent events
If the two events are totally unrelated, they are called independent events. For instance, the outcome of a coin flip is independent of whether the weather is rainy or sunny.
On the other hand, a rainy day depends and the presence of clouds are dependent events. The presence of clouds is likely to be predictive of a rainy day. In the same way, the appearance of the word Viagra is predictive of a spam email.
If all events were independent, it would be impossible to predict any event using data about other events. Dependent events are the basis of predictive modeling.
Mutually exclusive and collectively exhaustive
In probability theory and logic, a set of events is Mutually exclusive or disjoint if they cannot both occur at the same time. A clear example is the set of outcomes of a single coin toss, which can result in either heads or tails, but not both. https://en.wikipedia.org/wiki/Mutual_exclusivity
A set of events is jointly or collectively exhaustive if at least one of the events must occur. For example, when rolling a six-sided die, the events (each consisting of a single outcome) are collectively exhaustive, because they encompass the entire range of possible outcomes. https://en.wikipedia.org/wiki/Collectively_exhaustive_events
Is a set of events is Mutially exclusive and Collectively exhaustive, such as or , or and , then knowing the probability of outcomes reveals the probability of the remaining one. In other words, if there are two outcomes and we know the probability of one, then we automatically know the probability of the other: For example, given the value , we are able to calculate
Marginal probability
The marginal probability is the probability of a single event occurring, independent of other events. A conditional probability, on the other hand, is the probability that an event occurs given that another specific event has already occurred. https://en.wikipedia.org/wiki/Marginal_distribution
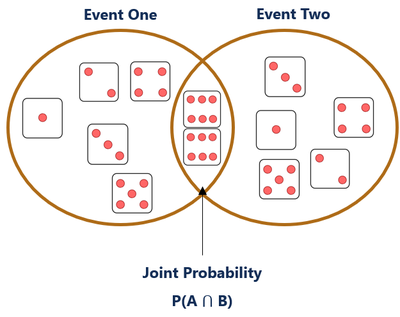
Joint Probability
Joint Probability (Independence)
For any two independent events A and B, the probability of both happening (Joint Probability) is:
Often, we are interested in monitoring several non-mutually exclusive events for the same trial. If some other events occur at the same time as the event of interest, we may be able to use them to make predictions.
In the case of spam detection, consider, for instance, a second event based on the outcome that the email message contains the word Viagra. This word is likely to appear in a spam message. Its presence in a message is therefore a very strong piece of evidence that the email is spam.
We know that of all messages were and of all messages contain the word . Our job is to quantify the degree of overlap between these two probabilities. In other words, we hope to estimate the probability of both and the word co-occurring, which can be written as .
If we assume that and are independent (note, however! that they are not independent), we could then easily calculate the probability of both events happening at the same time, which can be written as
Because of all messages are spam, and of all emails contain the word Viagra, we could assume that of the of spam messages contains the word . Thus, . of the represents of all messages . So, of all messages are
In reality, it is far more likely that and are highly dependent, which means that this calculation is incorrect. Hence the importance of the conditional probability.
Conditional probability
Conditional probability is a measure of the probability of an event occurring, given that another event has already occurred. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as , or sometimes or . https://en.wikipedia.org/wiki/Conditional_probability
For example, the probability that any given person has a cough on any given day may be only . But if we know or assume that the person is sick, then they are much more likely to be coughing. For example, the conditional probability that someone sick is coughing might be , in which case we would have that and . https://en.wikipedia.org/wiki/Conditional_probability
Kolmogorov definition of Conditional probability
Al parecer, la definición más común es la de Kolmogorov.
Given two events and from the sigma-field of a probability space, with the unconditional probability of being greater than zero (i.e., ), the conditional probability of given is defined to be the quotient of the probability of the joint of events and , and the probability of : https://en.wikipedia.org/wiki/Conditional_probability
Bayes s theorem
Also called Bayes' rule and Bayes' formula
Thomas Bayes (1763): An essay toward solving a problem in the doctrine of chances, Philosophical Transactions fo the Royal Society, 370-418.
Bayes's Theorem provides a way of calculating the conditional probability when we know the conditional probability in the other direction.
It cannot be assumed that . Now, very often we know a conditional probability in one direction, say , but we would like to know the conditional probability in the other direction, . https://web.stanford.edu/class/cs109/reader/3%20Conditional.pdf. So, we can say that Bayes' theorem provides a way of reversing conditional probabilities: how to find from and vice-versa.
Bayes's Theorem is stated mathematically as the following equation:
can be read as the probability of event given that event occurred. This is known as conditional probability since the probability of is dependent or conditional on the occurrence of event .
The terms are usually called:
| * | : | Likelihood [1]; |
Also called Update [2] |
|||
| * | : | Marginal likelihood; |
Also called Evidence [1]; |
Also called Normalization constant [2] | ||
| * | : | Prior probability [1]; | Also called Prior[2] | |||
| * | : | Posterior probability [1]; | Also called Posterior [2] |
Likelihood and Marginal Likelihood
When we are calculating the probabilities of discrete data, like individual words in our example, and not the probability of something continuous, like weight or height, these Probabilities are also called Likelihoods. However, in some sources, you can find the use of the term Probability even when talking about discrete data. https://www.youtube.com/watch?v=O2L2Uv9pdDA
In our example:
- The probability that the word 'Viagra' was used in previous spam messages is called the Likelihood.
- The probability that the word 'Viagra' appeared in any email (spam or ham) is known as the Marginal likelihood.
Prior Probability
Suppose that you were asked to guess the probability that an incoming email was spam. Without any additional evidence (other dependent events), the most reasonable guess would be the probability that any prior message was spam (that is, 20% in the preceding example). This estimate is known as the prior probability. It is sometimes referred to as the «initial guess»
Posterior Probability
Now suppose that you obtained an additional piece of evidence. You are told that the incoming email contains the word 'Viagra'.
By applying Bayes' theorem to the evidence, we can compute the posterior probability that measures how likely the message is to be spam.
In the case of spam classification, if the posterior probability is greater than 50 percent, the message is more likely to be spam than ham, and it can potentially be filtered out.
The following equation is the Bayes' theorem for the given evidence:
Applying Bayes' Theorem
Let's say that we are training a Span classifier.
We need information about the frequency of words in spam or ham (non-spam) emails. We will assume that the Naïve Bayes learner was trained by constructing a likelihood table for the appearance of these four words in 100 emails, as shown in the following table:
| Viagra | Money | Groceries | Unsubscribe | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Yes | No | Yes | No | Yes | No | Yes | No | Total | |
| Spam | 4/20 | 16/20 | 10/20 | 10/20 | 0/20 | 20/20 | 12/20 | 8/20 | 20 |
| Ham | 1/80 | 79/80 | 14/80 | 66/80 | 8/80 | 72/80 | 23/80 | 57/80 | 80 |
| Total | 5/100 | 95/100 | 24/100 | 76/100 | 8/100 | 92/100 | 35/100 | 65/100 | 100 |
As new messages are received, the posterior probability must be calculated to determine whether the messages are more likely to be spam or ham, given the likelihood of the words found in the message text.
Scenario 1 - A single feature
Suppose we received a message that contains the word :
We can define the problem as shown in the equation below, which captures the probability that a message is spam, given that the words 'Viagra' is present:
|
|
(Likelihood) | :
|
The probability that a spam message contains the term | |||
|
|
(Marginal likelihood) | :
|
The probability that the word appeared in any email (spam or ham) | |||
|
|
(Prior probability) | :
|
The probability that an email is Spam | |||
|
|
(Posterior probability) | :
|
The probability that an email is Spam given that contain the word | |||
| ||||||
Scenario 2 - Class-conditional independence
Suppose we received a new message that contains the words and :
For a number of reasons, this is computationally difficult to solve. As additional features are added, tremendous amounts of memory are needed to store probabilities for all of the possible intersecting events. Therefore, Class-Conditional independence can be assumed to simplify the problem.
Class-conditional independence
The work becomes much easier if we can exploit the fact that Naïve Bayes assumes independence among events. Specifically, Naïve Bayes assumes class-conditional independence, which means that events are independent so long as they are conditioned on the same class value.
Assuming conditional independence allows us to simplify the equation using the probability rule for independent events . This results in a much easier-to-compute formulation:
Es EXTREMADAMENTE IMPORTANTE notar que the independence assumption made in Naïve Bayes is Class-Conditional. This means that the words a and b appear independently, given that the message is spam (and also, given that the message is not spam). This is why we cannot apply this assumption to the denominator of the equation. This is, we CANNOT assume that because in this case the words are not conditioned to belong to one class (Span or Non-spam). Esto no me queda del todo claro. See this post: https://stats.stackexchange.com/questions/66079/naive-bayes-classifier-gives-a-probability-greater-than-1
We are not able to simplify the denominator. Therefore, what is done in Naïve Bayes is to calculate the nominator for both classes ( and ). Because that the denominator is the same for both, we are able to state that the class whose nominator is greater would have the greater conditional probability and therefore is the more likely class for the features given.
Because , we can say that this message is six times more likely to be spam than ham. However, to convert these numbers to probabilities, we need one last step.
The probability of spam is equal to the likelihood that the message is spam divided by the likelihood that the message is either spam or ham:
The presentation shows this example this way. I think there are mistakes in this presentation:
- Let's extend our spam filter by adding a few additional terms to be monitored: "money", "groceries", and "unsubscribe".
- We will assume that the Naïve Bayes learner was trained by constructing a likelihood table for the appearance of these four words in 100 emails, as shown in the following table:
As new messages are received, the posterior probability must be calculated to determine whether the messages are more likely to be spam or ham, given the likelihood of the words found in the message text.
We can define the problem as shown in the equation below, which captures the probability that a message is spam, given that the words 'Viagra' and Unsubscribe are present and that the words 'Money' and 'Groceries' are not.
Using the values in the likelihood table, we can start filling numbers in these equations. Because the denominatero si the same in both cases, it can be ignored for now. The overall likelihood of spam is then:
While the likelihood of ham given the occurrence of these words is:
Because 0.012/0.002 = 6, we can say that this message is six times more likely to be spam than ham. However, to convert these numbers to probabilities, we need one last step.
The probability of spam is equal to the likelihood that the message is spam divided by the likelihood that the message is either spam or ham:
The probability that the message is spam is 0.857. As this is over the threshold of 0.5, the message is classified as spam.
Scenario 3 - Laplace Estimator
Suppose we received another message, this time containing the terms: Viagra, Money, Groceries, and Unsubscribe.
Surely this is a misclassification? right?. This problem might arise if an event never occurs for one or more levels of the class. for instance, the term Groceries had never previously appeared in a spam message. Consequently,
This value causes the posterior probability of Spam to be zero, giving the presence of the word Groceries the ability to effectively nullify and overrule all of the other evidence.
Even if the email was otherwise overwhelmingly expected to be spam, the zero likelihood for the word Groceries will always result in a probability of spam being zero.
A solution to this problem involves using the Laplace estimator
The Laplace estimator, named after the French mathematician Pierre-Simon Laplace, essentially adds a small number to each of the counts in the frequency table, which ensures that each feature has a nonzero probability of occurring with each class.
Typically, the Laplace estimator is set to 1, which ensures that each class-feature combination is found in the data at least once. The Laplace estimator can be set to any value and does not necessarily even have to be the same for each of the features.
Using a value of 1 for the Laplace estimator, we add one to each numerator in the likelihood function. The sum of all the 1s added to the numerator must then be added to each denominator. The likelihood of spam is therefore:
While the likelihood of ham is:
This means that the probability of spam is and the probability of ham is ; a more plausible result that the one obtained when Groceries alone determined the result:
Naïve Bayes - Numeric Features
Because Naïve Bayes uses frequency tables for learning the data, each feature must be categorical in order to create the combinations of class and feature values comprising the matrix.
Since numeric features do not have categories of values, the preceding algorithm does not work directly with numeric data.
One easy and effective solution is to discretize numeric features, which simply means that the numbers are put into categories knows as bins. For this reason, discretization is also sometimes called binning.
This method is ideal when there are large amounts of training data, a common condition when working with Naïve Bayes.
There is also a version of Naïve Bayes that uses a kernel density estimator that can be used on numeric features with a normal distribution.
RapidMiner Examples
- Example 1:
- Example 2:
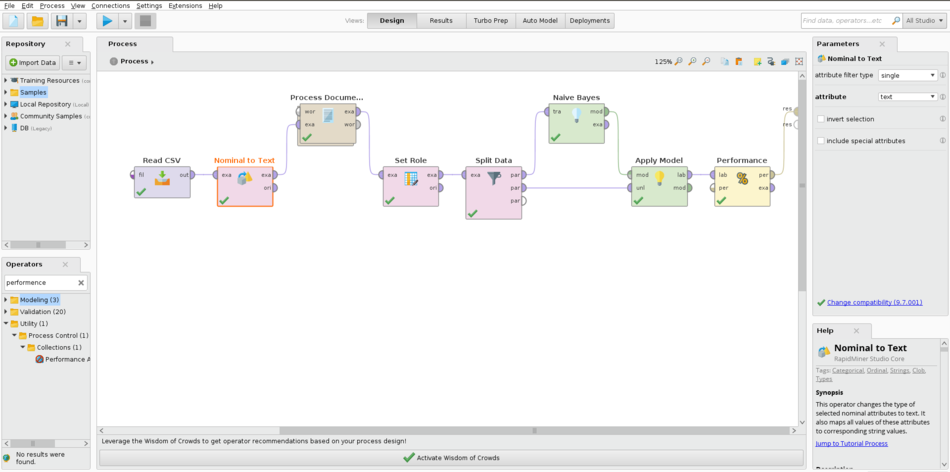
- Example 3: