Difference between revisions of "Página de pruebas 3"
Adelo Vieira (talk | contribs) (→Naive Bayes) (Tag: Blanking) |
Adelo Vieira (talk | contribs) |
||
| Line 1: | Line 1: | ||
| + | <br /> | ||
| + | {| class="wikitable" | ||
| + | |+ | ||
| + | |- | ||
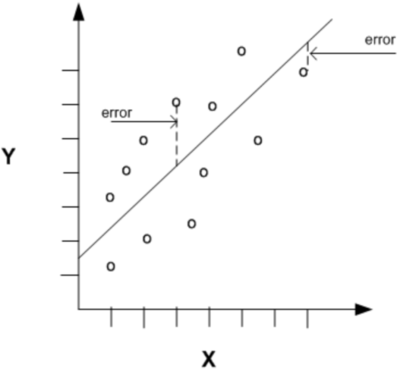
| + | ! style="vertical-align:top;" |<h5 style="text-align:left; vertical-align:top">Confusion Matrix or Coincidence Matrix</h5> | ||
| + | |[[File:Regression_errors.png|400px|center|]] | ||
| + | | | ||
| + | {| class="wikitable" | ||
| + | |+ | ||
| + | !<math>y</math> | ||
| + | !<math>\hat{y}</math> | ||
| + | !<math>\left \vert y - \hat{y} \right \vert</math> | ||
| + | |- | ||
| + | |5 | ||
| + | |6 | ||
| + | |1 | ||
| + | |- | ||
| + | |6.5 | ||
| + | |5.5 | ||
| + | |1 | ||
| + | |- | ||
| + | |8 | ||
| + | |9.5 | ||
| + | |1.5 | ||
| + | |- | ||
| + | |8 | ||
| + | |6 | ||
| + | |2 | ||
| + | |- | ||
| + | |7.5 | ||
| + | |10 | ||
| + | |2.5 | ||
| + | |} | ||
| + | |- | ||
| + | ! style="vertical-align:top;" |<h5 style="text-align:left; vertical-align:top">Mean Absolute Error - MAE</h5> | ||
| + | |The Mean Absolute Error (MAE) is calculated taking the sum of the absolute differences between the actual and predicted values (i.e. the errors with the sign removed) and multiplying it by the reciprocal of the number of observations. | ||
| + | Note that the value returned by the equation is dependent on the range of the values in the dependent variable. it ks '''scale dependent'''. | ||
| + | |||
| + | MAE is preferred by many as the evaluation metric of choice as it gives equal weight to all errors, irrespective of their magnitude. | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | <math> | ||
| + | MAE = \frac{}{} \sum_{i=1}^{n} \left \vert Y_i - \hat{Y}_i \right \vert | ||
| + | </math> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /><math> | ||
| + | Accuracy = \frac{72 + 24}{72 + 24 + 16 + 6} = \frac{96}{120} = 0.8 | ||
| + | </math> | ||
| + | </div> | ||
| + | </div> | ||
| + | |- | ||
| + | ! style="vertical-align:top;" |<h5 style="text-align:left; vertical-align:top">Mean Squared Error - MSE</h5> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | The Mean Squared Error (MSE) is very similar to the MAE, except that it is calculated taking the sum of the squared differences between the actual and predicted values and multiplying it by the reciprocal of the number of observations. Note that squaring the differences also removes their sign. | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | As with MAE, the value returned by the equation is dependent on the range of the values in the dependent variable. It is '''scale dependent'''. | ||
| + | </div> | ||
| + | </div> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | <math> | ||
| + | MSE = \frac{1}{n} \sum_{i=1}^n (Y_i - \hat{Y}_i)^2 | ||
| + | </math> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | <math> | ||
| + | Balanced Accuracy = \frac{\frac{72}{72 + 8} + \frac{24}{24 + 16} }{2} = \frac{0.9 + 0.6}{2} = 0.75 | ||
| + | </math> | ||
| + | </div> | ||
| + | </div> | ||
| + | |- | ||
| + | ! style="vertical-align:top;" |<h5 style="text-align:left; vertical-align:top">Root Mean Squared Error</h5> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | The Root Mean Squared Error (MSE) is basically the same as MSE, except that it is calculated taking the square root of sum of the squared differences between the actual and predicted values and multiplying it by the reciprocal of the number of observations. | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | As with MAE and MSE, the value returned by the equation is dependent on the range of the values in the dependent variable. It is '''scale dependent'''. | ||
| + | |||
| + | |||
| + | MSE and its related metric, RMSE, have been both criticized because they both give heavier weight to larger magnitude errors (outliers). However, this property may be desirable in some circumstances, where large magnitude errors are undesirable, even in small numbers. | ||
| + | </div> | ||
| + | </div> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | <math> | ||
| + | RMSE = \sqrt{\frac{1}{n} \sum_{i=i}^n (Y_i - \hat{Y}_i)^2 } | ||
| + | </math> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | <math>Sensitivity = \frac{72}{72 + 8} = 0.9</math> | ||
| + | |||
| + | <math>Sencitivity = \frac{24}{24 + 16} = 0.6</math> | ||
| + | </div> | ||
| + | </div> | ||
| + | |- | ||
| + | ! style="vertical-align:top;" |<h5 style="text-align:left; vertical-align:top">Mean Absolute Percentage Error</h5> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | Mean Absolute Percentage Error (MAPE) is a '''scale-independent''' measure of the performance of a regression model. It is calculated by summing the absolute value of the difference between the actual value and the predicted value, divided by the actual value. This is then multiplied by the reciprocal of the number of observations. This is then multiplied by 100 to obtain a percentage. | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | Although it offers a scale-independent measure, MAPE is not without problems: | ||
| + | * It can not be employed if any of the actual values are true zero, as this would result in a division by zero error. | ||
| + | * Where predicted values frequently exceed the actual values, the percentage error can exceed 100% | ||
| + | * It penalizes negative errors more than positive errors, meaning that models that routinely predict below the actual values will have a higher MAPE. | ||
| + | </div> | ||
| + | </div> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | <math> | ||
| + | MAPE = \frac{1}{n} \sum_{i=1}^n \left \vert \frac{Y_i - \hat{Y}_i}{Y_i} \right \vert \times 100 | ||
| + | </math> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | <math>Precision = \frac{72}{72 + 16} = 0.8182</math> | ||
| + | |||
| + | |||
| + | <math>Recall = \frac{72}{72 + 8} = 0.90</math> | ||
| + | </div> | ||
| + | </div> | ||
| + | |- | ||
| + | ! style="vertical-align:top;" |<h5 style="text-align:left; vertical-align:top">R squared</h5> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | <math>R^2</math>, or the Coefficient of Determination, is the ratio of the amount of variance explained by a model and the total amount of variance in the dependent variable and is the rage [0,1]. | ||
| + | |||
| + | |||
| + | Values close to 1 indicate that a model will be better at predicting the dependent variable. | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | R squared is calculated by summing up the squared differences between the predicted values and the actual values (the top part of the equation) and dividing that by the squared deviation of the actual values from their mean (the bottom part of the equation). The resulting value is then subtracted from 1. | ||
| + | |||
| + | |||
| + | A high <math>R^2</math> is not necessarily an indicator of a good model, as it could be the result of overfitting. | ||
| + | </div> | ||
| + | </div> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | <math> | ||
| + | R^2 = 1 - \frac{SS_{res}}{SS_{tot}} | ||
| + | = 1 - \frac{\sum_{i=1}^n(y_i - \hat{y}_i)^2}{\sum_{i=1}^n(y_i - \bar{y})^2} | ||
| + | </math> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | <math> | ||
| + | F1Score = \frac{2 \times 72}{2 \times 72 + 16 + 8} = 0.8571 | ||
| + | </math> | ||
| + | </div> | ||
| + | </div> | ||
| + | |- | ||
| + | ! style="vertical-align:top;" |<h5 style="text-align:left; vertical-align:top">Matthews Correlation Coefficient</h5> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | The F1-Score is adequate as a metric when precision and recall are considered equally important, or when the relative weighting between the two can be determined non-arbitrarily. | ||
| + | |||
| + | An alternative for cases where that does not apply is the '''Matthews Correlation Coefficient'''. It returns a value in the interval <math>[-1,+1]</math>, where -1 suggests total disagreement between predicted values and actual values, 0 is indicative that any agreement is the product of random chance and +1 suggests perfect prediction. | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | So, if the value is -1, every value that is true will be predicted as false and everyone that is false will be predicted as true. If the value is 1, every value that is true will be predicted as such and every value that is false will be predicted as such. | ||
| + | |||
| + | |||
| + | Unlike any of the metrics we have seen in previous slides, the Matthews Correlation coefficient takes into account all four categories in the confusion matrix. | ||
| + | </div> | ||
| + | </div> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | <math> | ||
| + | MCC = \frac{TP \times TN - FP \times FN}{\sqrt{(TP + FP) \times (TP + FN) \times (TN + FP) \times (TN + FN)}} | ||
| + | </math> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | <math> | ||
| + | MCC = \frac{1728 - 128}{\sqrt{88 \times 80 \times 40 \times 32}} = 0.5330 | ||
| + | </math> | ||
| + | </div> | ||
| + | </div> | ||
| + | |- | ||
| + | ! style="vertical-align:top;" |<h5 style="text-align:left; vertical-align:top">Cohen's Kappa</h5> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | Cohen's Kappa is a measure of the amount of agreement between two raters classifying N items into C mutually-exclusive categories. | ||
| + | |||
| + | |||
| + | It is defined by the equation given below, where <math>\rho_0</math> is the observed agreement between raters and <math>\rho_e</math> is the hypothetical agreement that would be expected to occur by random chance. | ||
| + | |||
| + | |||
| + | Landis and Koch (1977) suggest an interpretation of the magnitude of the results as follows: | ||
| + | |||
| + | <math> | ||
| + | \begin{array}{lcl} | ||
| + | 0 & = & \text{agreement equivalent to chance} \\ | ||
| + | 0.10 - 0.20 & = & \text{slight agreement} \\ | ||
| + | 0.21 - 0.40 & = & \text{fair agreement} \\ | ||
| + | 0.41 - 0.60 & = & \text{moderate agreement} \\ | ||
| + | 0.61 - 0.80 & = & \text{substantial agreement} \\ | ||
| + | 0.81 - 0.99 & = & \text{near perfect agreement} \\ | ||
| + | 1 & = & \text{perfect agreement} \\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | ... | ||
| + | </div> | ||
| + | </div> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | <math>K = 1 - \frac{1 - \rho_0}{1 - \rho_e}</math> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | *'''Calculate <math>\rho_0</math>'''<blockquote>The agreement on the positive class is 72 instances and on the negative class is 24 instances. So the agreement is 96 instances out of a total of 120<math>\rho_0 = \frac{96}{120} = 0.7</math> Note this is the same as the accuracy | ||
| + | |||
| + | *'''Calculate the probability of random agreement on the «positive» class:''' | ||
| + | |||
| + | <blockquote>The probability that both actual and predicted would agree on the positive class at random is the proportion of the total the positive class makes up for each of actual and predicted. | ||
| + | |||
| + | For the actual class, this is: | ||
| + | |||
| + | <math>\frac{(72 + 8)}{120} = 0.6666</math> | ||
| + | |||
| + | For the predicted class this is: | ||
| + | |||
| + | <math>\frac{(72 + 16)}{120} = 0.7333</math> | ||
| + | |||
| + | The total probability that both actual and predicted will randomly agree on the positive class is <math>0.6666 \times 0.7333 = 0.4888</math></blockquote> | ||
| + | |||
| + | *'''Calculate the probability of random agreement on the «negative» class:''' | ||
| + | |||
| + | <blockquote>The probability that both actual and predicted would agree on the negative class at random is the proportion of the total the negative class makes up for each of actual and predicted. | ||
| + | |||
| + | For the actual class, this is | ||
| + | |||
| + | <math>\frac{(16 + 24)}{120} = 0.3333</math> | ||
| + | |||
| + | For the predicted class this is | ||
| + | |||
| + | <math>\frac{(8 + 24)}{120} = 0.2666</math> | ||
| + | |||
| + | The total probability that both actual and predicted will randomly agree on the negative class is <math>0.3333 \times 0.2666 = 0.0888</math></blockquote> | ||
| + | |||
| + | *'''Calculate <math>\rho_e</math>''' | ||
| + | |||
| + | <blockquote>The probability <math>\rho_e</math> is simply the sum of the results of the calculations previously calculated: | ||
| + | |||
| + | <math>\rho_e = 0.4888 + 0.0888 = 0.5776</math></blockquote> | ||
| + | |||
| + | *'''Calculate kappa:''' | ||
| + | |||
| + | <blockquote> | ||
| + | <math> | ||
| + | K = 1 - \frac{1 - \rho_0}{1- \rho_e}</math> <math>= 1 - \frac{1 - 0.7}{1 - 0.5776} = 0.2898 | ||
| + | </math> | ||
| + | |||
| + | This indicates a 'fair agreement' according to the scale suggested by Lanis and Koch (1977) | ||
| + | </blockquote> | ||
| + | </div> | ||
| + | </div> | ||
| + | |- | ||
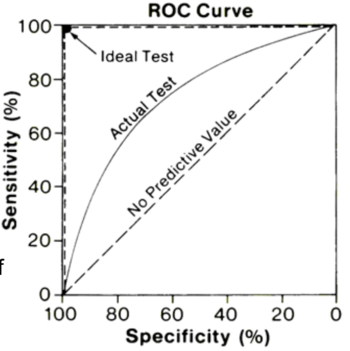
| + | ! style="vertical-align:top;" |<h5 style="text-align:left; vertical-align:top">The receiver Operator Characteristic Curve</h5> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | The Receiver Operating Characteristic Curve has its origins in radio transmission, but in this context is a method to visually evaluate the performance of a classifier. It is a 2D trap with the true positive rate on the x-axis and the false positive rate on the y-axis. | ||
| + | |||
| + | |||
| + | '''There are 4 keys points on a ROC curve:''' | ||
| + | |||
| + | * (0,0): classifier doesn't do anything | ||
| + | * (1,1): classifier always predict true | ||
| + | * (0,1): perfect classifier that never issues a false positive | ||
| + | * Line y = x: random classification (coin toss); the standards base line | ||
| + | |||
| + | |||
| + | '''Any classifier is:''' | ||
| + | |||
| + | * better the closer it is to the point (0,1) | ||
| + | * conservative if it is on the left-hand side of the graph | ||
| + | * liberal if they are in on the upper right of the graph | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | '''To create a ROC curve we do the following:''' | ||
| + | |||
| + | * Rank the prediction of ta classifier by confidence in (or probability of) correct classification | ||
| + | * Order them (highest first) | ||
| + | * Plot each prediction's impact on the true positive rate and false-positive rate. | ||
| + | |||
| + | |||
| + | Classifiers are considered conservative if they make positive classifications in the presence of strong evidence, so they make fewer false-positive errors, typically at the cost of low true positive rates. | ||
| + | |||
| + | Classifiers are considered liberal if they make positive classifications with weak evidence so they classify nearly all positives correctly, typically at the cost of high false-positive rates. | ||
| + | |||
| + | |||
| + | May real-world data sets are dominated by negative instances. The left-hand side of the ROC curve is, therefore, more interesting. | ||
| + | </div> | ||
| + | </div> | ||
| + | | | ||
| + | [[File:ROC_curve.png|center|350px]] | ||
| + | |- | ||
| + | !style="vertical-align:top;" |<h5 style="text-align:left; vertical-align:top">The Area Under the ROC Curve - AUC</h5> | ||
| + | | | ||
| + | <div class="mw-collapsible mw-collapsed" data-expandtext="+/-" data-collapsetext="+/-"> | ||
| + | Although the ROC curve can provide a Quik visual indication of the performance of a classifier, they can be difficult to interpret. | ||
| + | |||
| + | |||
| + | It is possible to reduce the curve to a meaningful number (a scalar) by computing the area under the curve. | ||
| + | |||
| + | |||
| + | AUC falls in the range [0,1], with 1 indicating a perfect classifier, 0.5 a classifier no better than a random choice and 0 a classifier that predicts everything incorrectly. | ||
| + | |||
| + | |||
| + | A convention for interpreting AUC is: | ||
| + | |||
| + | * 0.9 - 1.0 = A (outstanding) | ||
| + | * 0.8 - 0.9 = B (excellent / good) | ||
| + | * 0.7 - 0.8 = C (acceptable / fair) | ||
| + | * 0.6 - 0.7 = D (poor) | ||
| + | * 0.5 - 0.6 = F (no discrimination) | ||
| + | |||
| + | |||
| + | Note that ROC curves with similar AUCs may be shaped very differently, so the AUC can be misleading and shouldn't be computed without some qualitative examination of the ROC curve itself. | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <br /> | ||
| + | ... | ||
| + | </div> | ||
| + | </div> | ||
| + | | | ||
| + | |} | ||
| + | |||
| + | |||
| + | <br /> | ||
Revision as of 22:26, 3 July 2020
Contents
Confusion Matrix or Coincidence Matrix |
| |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Mean Absolute Error - MAE |
The Mean Absolute Error (MAE) is calculated taking the sum of the absolute differences between the actual and predicted values (i.e. the errors with the sign removed) and multiplying it by the reciprocal of the number of observations.
Note that the value returned by the equation is dependent on the range of the values in the dependent variable. it ks scale dependent. MAE is preferred by many as the evaluation metric of choice as it gives equal weight to all errors, irrespective of their magnitude. |
| ||||||||||||||||||
Mean Squared Error - MSE |
The Mean Squared Error (MSE) is very similar to the MAE, except that it is calculated taking the sum of the squared differences between the actual and predicted values and multiplying it by the reciprocal of the number of observations. Note that squaring the differences also removes their sign.
|
| ||||||||||||||||||
Root Mean Squared Error |
The Root Mean Squared Error (MSE) is basically the same as MSE, except that it is calculated taking the square root of sum of the squared differences between the actual and predicted values and multiplying it by the reciprocal of the number of observations.
|
| ||||||||||||||||||
Mean Absolute Percentage Error |
Mean Absolute Percentage Error (MAPE) is a scale-independent measure of the performance of a regression model. It is calculated by summing the absolute value of the difference between the actual value and the predicted value, divided by the actual value. This is then multiplied by the reciprocal of the number of observations. This is then multiplied by 100 to obtain a percentage.
|
| ||||||||||||||||||
R squared |
, or the Coefficient of Determination, is the ratio of the amount of variance explained by a model and the total amount of variance in the dependent variable and is the rage [0,1].
|
| ||||||||||||||||||
Matthews Correlation Coefficient |
The F1-Score is adequate as a metric when precision and recall are considered equally important, or when the relative weighting between the two can be determined non-arbitrarily. An alternative for cases where that does not apply is the Matthews Correlation Coefficient. It returns a value in the interval , where -1 suggests total disagreement between predicted values and actual values, 0 is indicative that any agreement is the product of random chance and +1 suggests perfect prediction.
|
| ||||||||||||||||||
Cohen's Kappa |
Cohen's Kappa is a measure of the amount of agreement between two raters classifying N items into C mutually-exclusive categories.
|
| ||||||||||||||||||
The receiver Operator Characteristic Curve |
The Receiver Operating Characteristic Curve has its origins in radio transmission, but in this context is a method to visually evaluate the performance of a classifier. It is a 2D trap with the true positive rate on the x-axis and the false positive rate on the y-axis.
Classifiers are considered liberal if they make positive classifications with weak evidence so they classify nearly all positives correctly, typically at the cost of high false-positive rates.
|
|||||||||||||||||||
The Area Under the ROC Curve - AUC |
Although the ROC curve can provide a Quik visual indication of the performance of a classifier, they can be difficult to interpret.
|
















![{\displaystyle [-1,+1]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/daa72f1a806823ec94fda7922597b19cbda684f4)