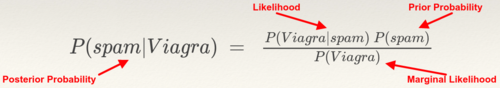Página de pruebas 3

Naive Bayes

Lecture and Tutorial: https://moodle.cct.ie/mod/scorm/player.php?a=4&currentorg=tuto&scoid=8&sesskey=wc2PiHQ6F5&display=popup&mode=normal

Note, on all the Naive Bayes examples given, the Performance operator is Performance (Binomial Classification)

Naïve Bayes is a classification technique that uses data about prior events to derive a probability of future events.

A common application of the algorithm uses the frequency of the occurrence of words in past emails to identify junk email. Bayesian classifiers utilize training data to calculate an observed probability for each class based on feature values. When such classifiers are later used on unlabeled data, they use those observed probabilities to predict the most likely class, given the features in the new data

It is a very simple idea, but it gives us a classification method that often delivers results on par with more sophisticated algorithms.

Bayesian classifiers have been used for:

• Text classification, such as spam filtering, author identification, and topic modeling
• Intrusion detection and anomaly detection on computer networks
• Diagnosis of medical conditions, given a set of observed symptoms.

Bayesian classifiers are typically best applied to problems in which the information from numerous attributes should be considered simultaneously in order to estimate the probability of an outcome. While many algorithms ignore features that have weak effects, Bayesian methods utilize all available evidence to subtly change the predictions.

If a large number of features have relatively minor effects, taken together their combined impact could be quite large. Bayesian probability theory is rooted in the idea that the estimated likelihood of an event should be based on the evidence at hand.

Events are possible outcomes, such as sunny and rainy weather, a heads or tails result in a coin flip, or spam and not spam email messages.

A trial is a single opportunity for the event to occur, such as a day's weather, a coin flip, or an email message. Naive Bayes

A common example:

In a TV weather forecast, precipitation is typically described using terms such as "60 percent chance of rain."

Such forecasts are based on probabilistic methods - methods concerned with quantifying uncertainty. They use data on past events to predict future events.

In the case of weather, the chance of rain describes the proportion of prior days with similar measurable atmospheric conditions in which precipitation occurred.

A 60 percent chance of rain, therefore, suggests that in 6 out of 10 days on record where there were similar atmospheric conditions, it rained.

Probability Primer

The probability of an event can be estimated from observed data by dividing the number of trials in which an event occurred by the total number of trials.

• For instance, if it rained 3 out of 10 days, the probability of rain can be estimated as 30 percent.
• Similarly, if 10 out of 50 email messages are spam, then the probability of spam can be estimated as 20 percent.
• The notation P(A) is used to denote the probability of event A, as in P(spam) = 0.20

Mutually exclusive and collectively exhaustive

Events are mutually exclusive and collectively exhaustive.

In probability theory and logic, a set of events is Mutually exclusive or disjoint if they cannot both occur at the same time. A clear example is the set of outcomes of a single coin toss, which can result in either heads or tails, but not both. https://en.wikipedia.org/wiki/Mutual_exclusivity

A set of events is jointly or collectively exhaustive if at least one of the events must occur. For example, when rolling a six-sided die, the events 1, 2, 3, 4, 5, and 6 (each consisting of a single outcome) are collectively exhaustive, because they encompass the entire range of possible outcomes. https://en.wikipedia.org/wiki/Collectively_exhaustive_events

If a trial has n outcomes that cannot occur simultaneously, such as heads or tails, or spam and ham (non-spam), then knowing the probability of n-1 outcomes reveals the probability of the remaining one.

In other words, if there are two outcomes and we know the probability of one, then we automatically know the probability of the other. For example, given the value P(spam) = 0.20 , we are able to calculate P(ham) = 1 – 0.20 = 0.80

Joint Probability

Often, we are interested in monitoring several non-mutually exclusive events for the same trial. If some other events occur at the same time as the event of interest, we may be able to use them to make predictions.

In the case of spam detection, consider, for instance, a second event based on the outcome that the email message contains the word Viagra. For most people, this word is only likely to appear in a spam message. Its presence in a message is therefore a very strong piece of evidence that the email is spam.

We know that 20 percent of all messages were spam and 5 percent of all messages contained the word "Viagra".

Our job is to quantify the degree of overlap between these two probabilities.

In other words, we hope to estimate the probability of both spam and the word "Viagra" co-occurring, which can be written as P(spam ∩ Viagra).

Calculating P(spam ∩ Viagra) depends on the joint probability of the two events, or how the probability of one event is related to the probability of the other.

If the two events are totally unrelated, they are called independent events.

For instance, the outcome of a coin flip is independent from whether the weather is rainy or sunny.

If all events were independent, it would be impossible to predict any event using data about other events. On the other hand, dependent events are the basis of predictive modeling.

For instance, the presence of clouds is likely to be predictive of a rainy day, and the appearance of the word Viagra is predictive of a spam email.

Joint Probability - Independence

If we assume that P(spam) and P(Viagra) are independent, we could then easily calculate P(spam ∩ Viagra) - the probability of both events happening at the same time.

Note that they are not independent, however!

Because 20 percent of all messages are spam, and 5 percent of all emails contain the word Viagra, we could assume that 5 percent of 20 percent (0.05 * 0.20 = 0.01 ), or 1 percent of all messages are spam contain the word Viagra.

More generally, for any two independent events A and B, the probability of both happening is: P(A ∩ B) = P(A) * P(B)

In reality, it is far more likely that P(spam) and P(Viagra) are highly dependent, which means that this calculation is incorrect. So we need to employ conditional probability.

Conditional probability - The Bayes' Theorem

Thomas Bayes (1763): An essay toward solving a problem in the doctrine of chances, Philosophical Transactions fo the Royal Society, 370-418.

The relationship between dependent events can be described using Bayes' Theorem, as shown in the following equation.

$P(A|B)={\frac {P(A\cap B)}{P(B)}}={\frac {P(B|A)P(A)}{P(B)}}$

The notation P(A|B) can be read as the probability of event A given that event B occurred. This is known as conditional probability, since the probability of A is dependent or conditional on the occurrence of event B.

Prior Probability

Suppose that you were asked to guess the probability that an incoming email was spam. Without any additional evidence, the most reasonable guess would be the probability that any prior message was spam (that is, 20 percent in the preceding example). This estimate is known as the prior probability.

Likelihood and Marginal Likelihood

Now suppose that you obtained an additional piece of evidence. You are told that the incoming email contains the word 'Viagra'.

• The probability that the word 'Viagra' was used in previous spam messages is called the likelihood.
• The probability that the word 'Viagra' appeared in any email (spam or ham) is known as the marginal likelihood.

Posterior Probability

By applying Bayes' theorem to the evidence, we can compute the posterior probability that measures how likely the message is to be spam.

In the case of spam classification, if the posterior probability is greater than 50 percent, the message is more likely to be spam than ham, and it can potentially be filtered out.

The following equation is the Bayes' theorem for the given evidence:

Applying Bayes' Theorem - Example

We need information on how frequently Viagra has occurred as spam or ham. Let's assume these numbers:

	Viagra
Frequency	Yes	No	Total
Spam	4	16	20
Ham	1	79	80
Total	5	95	100

• The likelihood table reveals that P(Viagra|spam) = 4/20 = 0.20, indicating that the probability is 20 percent that a spam message contains the term Viagra.
• Additionally, since the theorem says that P(B|A) x P(A) = P(A ∩ B), we can calculate P(spam ∩ Viagra) as P(Viagra|spam) x P(spam) = (4/20) x (20/100) = 0.04.
• This is four times greater than the previous estimate under the faulty independence assumption.

To compute the posterior probability we simply use:

$P(spam|Viagra)={\frac {P(Viagra|spam)P(spam)}{P(Viagra)}}={\frac {4/20\times 20/10}{5/100}}={\frac {0.2\times 0.2}{0.05}}=0.8$

• Therefore, the probability is 80 percent that a message is spam, given that it contains the word "Viagra".
• Therefore, any message containing this term should be filtered.

Applying Bayes' Theorem - Example

• Let's extend our spam filter by adding a few additional terms to be monitored: "money", "groceries", and "unsubscribe".
• We will assume that the Naïve Bayes learner was trained by constructing a likelihood table for the appearance of these four words in 100 emails, as shown in the following table:

As new messages are received, the posterior probability must be calculated to determine whether the messages are more likely to be spam or ham, given the likelihood of the words found in the message text. For example, suppose that a message contains the terms Viagra and Unsubscribe, but does not contain either Money or Groceries. Using Bayes' theorem, we can define the problem as shown in the equation on the next slide, which captures the probability that a message is spam, given that the words 'Viagra' and Unsubscribe are present and that the words 'Money' and 'Groceries' are not.

As mentioned on the previous slide, using Bayes' theorem, we can define the problem as shown in the equation below, which captures the probability that a message is spam, given that the words 'Viagra' and Unsubscribe are present and that the words 'Money' and 'Groceries' are not.

$P(Spam|Viagre\cap \urcorner Money\cap \urcorner Groceries\cap Unsubscribe)={\frac {P(Viagra\cap \urcorner Money\cap \urcorner Groceries\cap Unsubscribe|spam)P(spam)}{P(Viagra\cap \urcorner Money\cap \urcorner Groceries\cap Unsubscribe)}}$

For a number of reasons, this is computationally difficult to solve. As additional features are added, tremendous amounts of memory are needed to store probabilities for all of the possible intersecting events.

Class-Conditional Independence

The work becomes much easier if we can exploit the fact that Naïve Bayes assumes independence among events. Specifically, Naïve Bayes assumes class-conditional independence, which means that events are independent so long as they are conditioned on the same class value.

Assuming conditional independence allows us to simplify the equation using the probability rule for independent events, which you may recall is P(A ∩ B) = P(A) * P(B). This results in a much easier-to-compute formulation:

Using the values in the likelihood table, we can start filling numbers in these equations. Because the denominatero si the same in both cases, it can be ignored for now. The overall likelihood of spam is then:

${\frac {4}{20}}\times {\frac {10}{20}}\times {\frac {20}{20}}\times {\frac {12}{20}}\times {\frac {20}{100}}=0.012$

While the likelihood of ham given the occurrence of these words is:

${\frac {1}{80}}\times {\frac {60}{80}}\times {\frac {72}{80}}\times {\frac {23}{80}}\times {\frac {80}{100}}=0.002$

Because 0.012/0.002 = 6, we can say that this message is six times more likely to be spam than ham. However, to convert these numbers to probabilities, we need one last step.

The probability of spam is equal to the likelihood that the message is spam divided by the likelihood that the message is either spam or ham:

${\frac {0.012}{(0.012+0.002)}}=0.857$

The probability that the message is spam is 0.857. As this is over the threshold of 0.5, the message is classified as spam.

Naïve Bayes - Problems

Suppose we received another message, this time containing the terms: Viagra, Money, Groceries, and Unsubscribe. The likelihood table of spam is:

${\frac {4}{20}}\times {\frac {10}{20}}\times {\frac {0}{20}}\times {\frac {12}{20}}\times {\frac {20}{100}}=0$

Surely this is a misclassification? right?. This problem might arise if an event never occurs for one or more levels of the class. for instance, the term Groceries had never previously appeared in a spam message. Consequently, P(spam|groceries) = 0%

Because probabilities in Naïve Bayes are multiplied out, this 0% value causes the posterior probability of spam to be zero, giving the presence of the word Groceries the ability to effectively nullify and overrule all of the other evidence.

Even if the email was otherwise overwhelmingly expected to be spam, the zero likelihood for the word Groceries will always result in a probability of spam being zero.

Naïve Bayes - Laplace Estimator

A solution to this problem involves using something called the Laplace estimator, named after the French mathematician Pierre-Simon Laplace. The Laplace estimator essentially adds a small number to each of the counts in the frequency table, which ensures that each feature has a nonzero probability of occurring with each class.

Typically, the Laplace estimator is set to 1, which ensures that each class-feature combination is found in the data at least once. The Laplace estimator can be set to any value and does not necessarily even have to be the same for each of the features.

Using a value of 1 for the Laplace estimator, we add one to each numerator in the likelihood function. The sum of all the 1s added to the numerator must then be added to each denominator. The likelihood of spam is therefore:

${\frac {5}{24}}\times {\frac {11}{24}}\times {\frac {1}{24}}\times {\frac {13}{24}}\times {\frac {20}{100}}=0.0004$

While the likelihood of ham is:

${\frac {2}{84}}\times {\frac {15}{84}}\times {\frac {9}{84}}\times {\frac {24}{84}}\times {\frac {80}{100}}=0.0001$

This means that the probability of spam is 80 percent and the probability of ham is 20 percent; a more plausible result that the one obtained when Groceries alone determined the result.

Naïve Bayes - Numeric Features

Because Naïve Bayes uses frequency tables for learning the data, each feature must be categorical in order to create the combinations of class and feature values comprising the matrix.

Since numeric features do not have categories of values, the preceding algorithm does not work directly with numeric data.

One easy and effective solution is to discretize numeric features, which simply means that the numbers are put into categories knows as bins. For this reason, discretization is also sometimes called binning.

This method is ideal when there are large amounts of training data, a common condition when working with Naïve Bayes.

There is also a version of Naïve Bayes that uses a kernel density estimator that can be used on numeric features with a normal distribution.