Difference between revisions of "Calculus"
Adelo Vieira (talk | contribs) (Created page with "* '''Infinitesimal calculus''' (Math of change) (The study of things that change) https://en.wikipedia.org/wiki/Calculus : https://www.youtube.com/watch?v=w3GV9pumczQ :* '''D...") |
Adelo Vieira (talk | contribs) (→Differential calculus) |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | * '''Infinitesimal calculus''' | + | * '''Infinitesimal calculus''' |
| − | : https://www.youtube.com/watch?v=w3GV9pumczQ | + | :* Math of change |
| + | :* The study of things that change | ||
| + | :* Infinitesimal calculus allows us to study problems in which there are changes in the variables (or properties) involved in the problem. In other words, it allows us to mathematically describe changes. So, if we have a system that is changing, we can mathematically model it (or describe it) by using calculus. | ||
| + | :* https://en.wikipedia.org/wiki/Calculus | ||
| + | :* https://www.youtube.com/watch?v=w3GV9pumczQ | ||
| + | :* https://www.youtube.com/watch?v=MltYNJcCS14 | ||
| + | :* https://www.youtube.com/watch?v=4fqVT-DfpGg | ||
| + | |||
:* '''Differential calculus''' (Derivative) https://en.wikipedia.org/wiki/Differential_calculus | :* '''Differential calculus''' (Derivative) https://en.wikipedia.org/wiki/Differential_calculus | ||
| Line 9: | Line 16: | ||
:* One of the applications of Mathematical analysis (Calculus in particular) is for '''Signal processing''' | :* One of the applications of Mathematical analysis (Calculus in particular) is for '''Signal processing''' | ||
| + | |||
| + | |||
| + | It is not so easy to understand the difference between Algebra and Calculus. Let's try to explain it using an example in which we use math to study a physical problem: https://www.youtube.com/watch?v=MltYNJcCS14 | ||
| + | |||
| + | '''Algebra problem:''' A car moves at a constant speed and goes 180 miles in 3 hours. How fast is it going? | ||
| + | |||
| + | '''Calculus problem:''' A car moves with '''variable''' speed. Its position is given by s(t) = (some formula). Find its speed as a function of time. | ||
| + | |||
| + | |||
| + | <br /> | ||
| + | ==Differential calculus== | ||
| + | https://en.wikipedia.org/wiki/Differential_calculus | ||
| + | |||
| + | |||
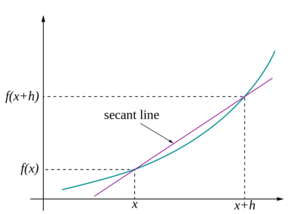
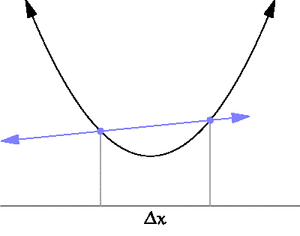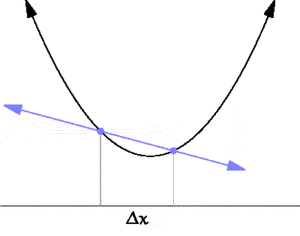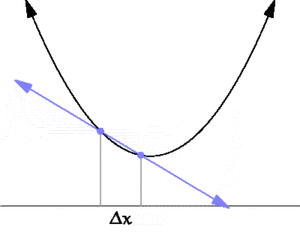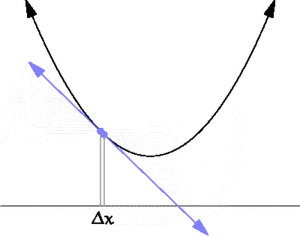
| + | [[File:Secant-calculus.png|thumb|300px|A secant approaches a tangent when <math>\Delta x \to 0</math>. Taken from https://en.wikipedia.org/wiki/Derivative]] | ||
| + | |||
| + | [[File:Tangent animation.gif|thumb|300px|A secant approaches a tangent when <math>\Delta x \to 0</math>. Taken from https://en.wikipedia.org/wiki/Derivative]] | ||
| + | |||
| + | |||
| + | Differential calculus is the study of the definition, properties, and applications of the derivative of a function. The process of finding the derivative is called differentiation. | ||
| + | |||
| + | |||
| + | |||
| + | <br /> | ||
Latest revision as of 21:09, 5 September 2020
- Infinitesimal calculus
- Math of change
- The study of things that change
- Infinitesimal calculus allows us to study problems in which there are changes in the variables (or properties) involved in the problem. In other words, it allows us to mathematically describe changes. So, if we have a system that is changing, we can mathematically model it (or describe it) by using calculus.
- https://en.wikipedia.org/wiki/Calculus
- https://www.youtube.com/watch?v=w3GV9pumczQ
- https://www.youtube.com/watch?v=MltYNJcCS14
- https://www.youtube.com/watch?v=4fqVT-DfpGg
- Differential calculus (Derivative) https://en.wikipedia.org/wiki/Differential_calculus
- Integral calculus https://en.wikipedia.org/wiki/Integral
- Fundamental theorem of calculus https://en.wikipedia.org/wiki/Fundamental_theorem_of_calculus
- One of the applications of Mathematical analysis (Calculus in particular) is for Signal processing
It is not so easy to understand the difference between Algebra and Calculus. Let's try to explain it using an example in which we use math to study a physical problem: https://www.youtube.com/watch?v=MltYNJcCS14
Algebra problem: A car moves at a constant speed and goes 180 miles in 3 hours. How fast is it going?
Calculus problem: A car moves with variable speed. Its position is given by s(t) = (some formula). Find its speed as a function of time.
Differential calculus
https://en.wikipedia.org/wiki/Differential_calculus
Differential calculus is the study of the definition, properties, and applications of the derivative of a function. The process of finding the derivative is called differentiation.